Marginal Cost Formula for Continuous Operation
Marginal cost is calculated by dividing the change in total cost by the change in quantity. Let us say that Business A is producing 100 units at a cost of $100. The business then produces at additional 100 units at a cost of $90. So the marginal cost would be the change in total cost, which is $90. Divided by the change in quantity, which is the additional 100 units. That gives us: $90/100, which equals $0.90 per unit as the marginal cost.
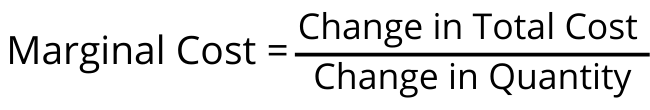
So what does change in total cost mean? Well, the marginal cost looks at the difference between two points of production. So how much extra does it cost to produce one unit instead of two units? The change in total cost is therefore calculated by taking away the total cost at point B from the total cost at point A.
For example, Business A produces 100 motor vehicles that cost $10,000 each, bringing the total cost to $1,000,000 or $1 million for short. If the firm then goes on to produce 120 more motor vehicles – costing them $1.2 million, we need to work out the difference between the total cost after ($1.2 million) and subtract it from the initial cost ($1 million), to get the change in total cost ($0.2 million).
Calculating a change in quantity involves looking at point A and point B in production and working out the difference. For instance, a business is going to be producing more and more goods as demand increases. However, it is necessary to look at how many more goods are sold between two points in order to calculate how this impacts on final profits.
If we look at the prior example, Business A went from producing 100 cars to 120. Therefore, the change in quantity would be the new quantity produced (120), minus the old quantity produced (100). This equals 20, which will then be used within the formula.
John Monroe owns a privately owned business called Monroes Motorbikes. In his first year of business, he produces and sells 10 motorbikes for $100,000, which cost him $50,000 to make. In his second year, he goes on to produce and sell 15 motorbikes for $150,000, which cost $75,000 to make.
First, we work out the change in the total cost. In this case, there was an increase from $50,000 to $75,000 – which works out as an increase of $25,000. Then we calculate the change in quantity which increases from 10 to 15; an increase of 5. We then divide the change in the total price ($25,000) by the change in quantity (5), which equals a marginal cost of $5,000 per motorbike.
Bob Ryan owns a bakery in central London. He has a number of fixed costs such as rent and the cost of purchasing machinery, tills, and other equipment. He then has a number of variable costs such as staff, utility bills, and raw materials.
In the first year of business, his total costs amount to $100,000, which include $80,000 of fixed costs and $20,000 of variable costs. He manages to sell 50,000 goods, making $200,000 in revenue.
In the second year of business, total costs increase to $120,000, which include $85,000 of fixed costs and $35,000 of variable costs. He manages to sell 75,000 goods, making $300,000 in revenue.
As we can see, fixed costs increase because new equipment is needed to expand production. Variable costs also increase as more staff and raw materials are needed. Both combine to create an increase in costs of $20,000. At the same time, the number of goods produced and sold increases by 25,000. The marginal cost of these is therefore calculated by dividing the additional cost ($20,000) by the increase in quantity (25,000), to reach a cost of $0.80 per unit.
Julie Porter owns a textile company that makes 200 dresses each year, which costs $15,000 to make these. She starts to experience an increase in demand, with an additional 20 dresses being requested. As a result, she wants to work out if it's worth her while to make these additional dresses.
She calculates the materials and other costs and finds out that it would cost her an additional $2,000 to make an extra 20 dresses. These marginal costs can then be calculated by dividing the costs by the quantity. So $2,000 / 20, which equals $100 per dress.
In order for her to be able to make a profit, she would, therefore, have to request the customers pay over $100 for each dress.
Marginal cost pricing is where the selling company reduces the price of its goods to equal marginal cost. In other words, it reduces the price so much that it no longer makes a profit on it. Usually, a firm would do this if they are suffering from weak demand, so reduce prices to marginal cost to attract customers back.
Alternatively, the business may be suffering from a lack of cash so need to sell their products quickly in order to get some cash on hand. It may be to pay for an upcoming debt payment, or, it might just be suffering from illiquidity. At the same time, it might operate a marginal cost pricing strategy to reduce stock – which is particularly common in fashion.
We often see supermarkets employ such a strategy. This might be in order to get rid of stock that is going out of date, or, to attract customers to purchase cheap goods. Whilst in the store, the idea is that they would also purchase other products that offer the firm a profit.
Source: https://boycewire.com/marginal-cost-definition/
0 Response to "Marginal Cost Formula for Continuous Operation"
Post a Comment